Wordle 最大化熵的開局兩手

作者： 李柏南 Po-Nan Li

沒想到我真的會再寫一篇關於 Wordle 的文章 XD

ＴＬＤＲ：如果你可以忍住不受第一猜的結果影響固定前兩步都用 DARNS 和 TOILE 的話，可以得到最大的期望資訊量！

以下正文無雷

前陣子看到泛科學介紹到知名數學 YouTuber 3brown1blue （下稱 3b1b）假借 Wordle 之名介紹了 information theory 以及 entropy 的概念。我雖然當下真是拍斷大腿，心想：哎呀，其實我也有想到完全一樣的數學策略，不過我是真的沒有寫下來（絕對不是因為手邊沒有紙！），而且人家影片漂漂亮亮地把我心裡想講的話講出來了，當然是高興都來不及了。

其實我並沒有受過正規的 information theory 教育，只有從 bioinformatics 的課程中學到一些皮毛，所以我自己也從 3b1b 的影片中溫習了一些已經生疏的觀念。簡單來說假設有一天你開局猜了 ZEBRA，雖然沒有天胡，不過第一個字竟然是綠色的，那表示你已經排除了超過 99% 的候選字，這個 Z 的訊息含量就非常地高。相對地如果你開局猜了 WEARY，確實得知了母音可能是 A，但是其實限縮的效果就比較有限。實際上猜 WEARY 或者 ZEBRA 都不是很理想，因為 Z 或者 W 的出現機率都不高，對於有心想要在四步甚至三步內破關的人來說，可能只是繞遠路而已。

那麼怎樣才能用統計的方法評估一個字的資訊含量呢？假設我們有興趣的開局字是 q，當天的謎底是 a，然後我們有一個函數 wordle(q, a) 可以回傳比對的結果。例如我開始玩 Wordle 的第一天，我的第一猜是 q=“APPLE”，答案是 a=“POINT”，那 wordle() 在我第一猜後就會回傳 “XBXXX”。實際上不只 APPLE 一個字會有 “XBXXX” 的結果，因此所有會產生 “XBXXX” = wordle(q, a=“APPLE”) 的 q 的集合，就是我們藉由 “XBXXX” 這個新的資訊得到的產物。針對每一個 q 我們考慮答案是任何一個合法的 a 的情況下能得到的資訊，再跟每個可能的輸出（也就是資訊）各字的機率相乘後加總，就是一個對於一個 q 的綜合評分（也就是 q 的 entropy）。

昨天 Eric 突然問我，是不是可以算出來一組固定的兩步開局法，從而得到最大的資訊量？

這邊又要回到 3b1b 的影片，他利用前面討論的觀念，得到了 TARES 這個字可以在第一步得到最多資訊的結論。TARES 這個字的平均資訊量是 6.19 bits，粗略地來說就是無論今天的謎底是什麼，平均來說我們可以把候選字縮小到 1/73 的範圍。無獨有偶，3b1b 也用了我前一篇文章推薦的 SLATE 作為對照，SLATE 的平均資訊量是 5.87 bits，大約可以把候選字限縮到 1/58.5 的範圍。

（使用 TARES 後可能得到的資訊量，限縮範圍越大的輸出結果資訊量越大，但是相對的發生的機率也越低）

所以 Eric 的問題可以理解為：假設我們的開局策略是用固定的兩個字當作前兩猜，那這樣可以得到多大的資訊量？他也問了，這兩個字會跟 TARES 或者其他高分字很類似嗎？

我先說結論：最高分的一組字是 DARNS 和 TOILE，他們組合起來的分數是 10.26 bits，也就是可以把候選字縮小到 1/1228 的範圍！如果這樣聽起來還不夠厲害，換句話說，平均來說使用了這組字之後，你會把候選字限縮到從 10.5 個字中去選。

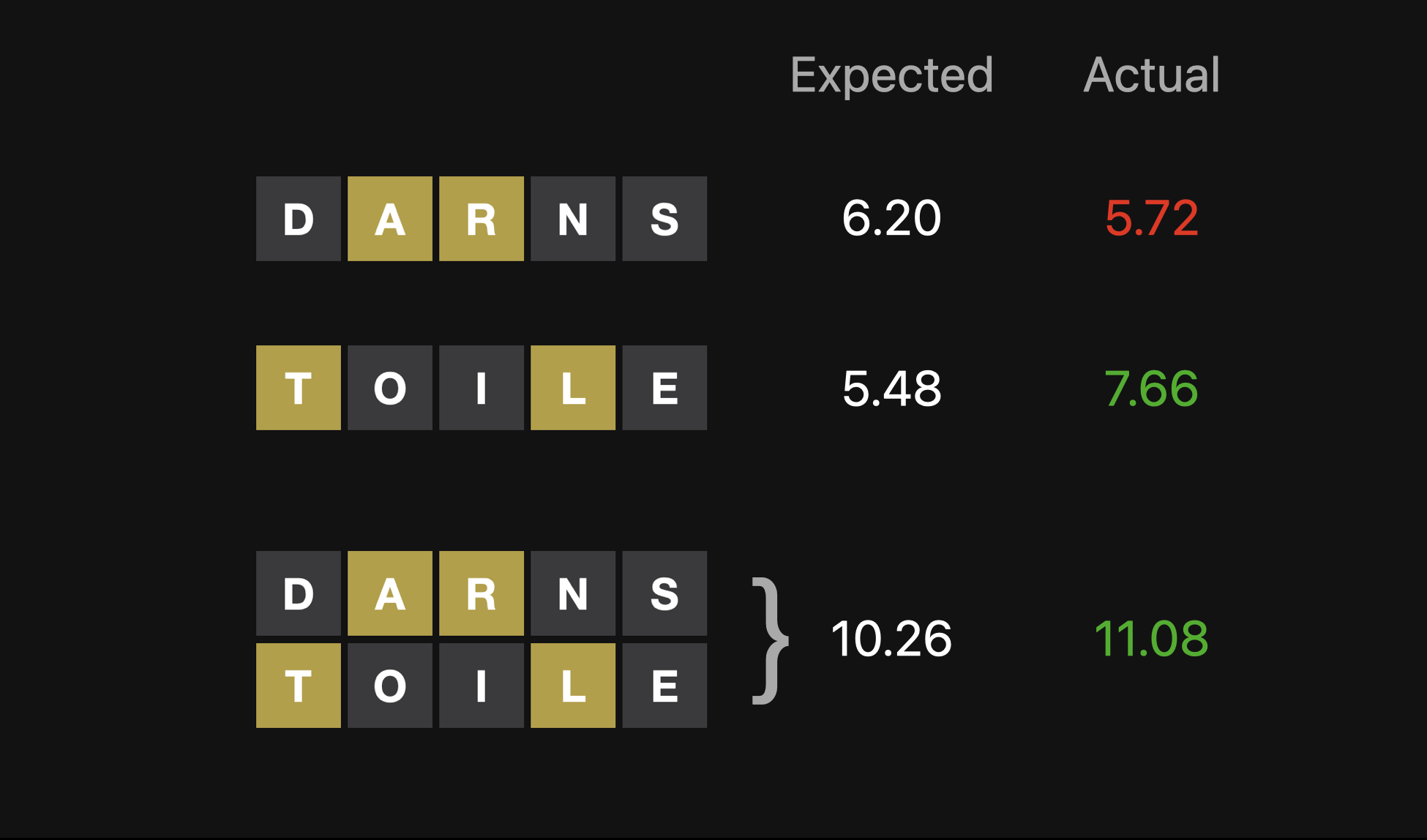
當然 3b1b 也討論到了，這樣的算法只是一個期望值，根據當天的謎底，你有可能運氣很好縮小到更小範圍，也有可能會沒有得到預期中的限縮效果。例如前面說到的 TARES 價值 6.19 bits，但若當天的謎底是 BIGGS，雖然輸出是 “XXXXA” 看起來很爽，但因為符合的字太多了，所以得到的資訊量只有 4.00 bits 而已。

話說回來，為什麼要去算這樣的兩步開局法呢？因為網路上各家討論的搜尋或者數學策略，除了能提供第一猜的建議之外，就只能拿來寫成機器人用。當然除了機器人之外，也可以做互動式的查詢程式或者直接用 javascript 做一個外掛，但是這些免不了都有作弊的嫌疑。就算有最佳化的第一猜，效果還是有限。但是如果固定的前兩猜可以可靠且有效地縮小範圍，那就值得把這兩個字背起來，從第三猜再開始把自己的情感放進來品味這個遊戲的策略。

至於有沒有方法可以證明這個兩步開局的策略優於同樣使用訊息理論但是只用一步開局呢？雖然這個策略設計的初衷是想要給人類玩家參考，但是在開局後讓大家用自己本來的策略來玩，不過就像我們可以模擬一步開局而且一路都用最大化 entropy 的策略，同樣的模擬方法也可以適用在兩步開局的策略，只要把前兩步都鎖死成 DARNS 跟 TOILE 就好了。我模擬的結果跟 3b1b 一模一樣，如果用第一步固定開局的玩法，平均可以在 4.0968 步內完成，改成用前兩步都固定的開局玩法的話，則「退步」到平均要 4.1061 步才會完成，可以說是並沒有比較差！雖然固定前兩步的話等於白白浪費一次動態搜尋的機會，且本來固定一步的策略會有 36 題可以直接兩步猜中，但是一步的策略會有 105 題會失敗（最差會花 12 步才猜完），固定兩步的策略可以把失敗的題目縮小到 72 題，等於多成功 33 題，算是蠻大的進步。

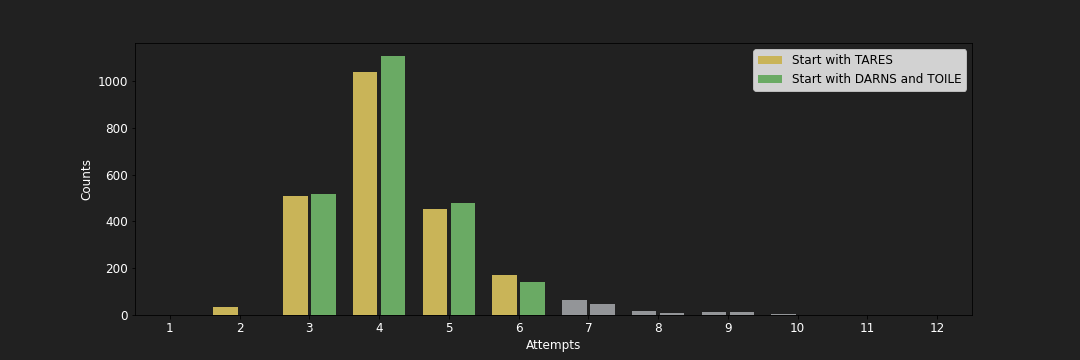
固定兩步開局的策略是設計給人類玩家用的，一但開局完成後，就可以用自己喜歡的玩法玩下去，具體的成效可能很難量化。不過大家可能會多或少都有遇過最後子音鬼打牆的狀況（例如 PILL/WILL/BILL/DILL/FILL/HILL/JILL/KILL），其實運用訊息理論的精神之一就是可以在早期避免大家走進這樣的死胡同。

以下是前幾高分的開局字組合及對應的 entropy

DARNS	TOILE	10.262
DAINT	LORES	10.255
PAREN	TOILS	10.248
LOINS	TARED	10.246
LARIS	TONED	10.242

以下是根據 3b1b 原本的算法 前幾高分的字及其 entropy

TARES	6.196
LARES	6.151
RALES	6.116
RATES	6.098
TERAS	6.078